应用麦克斯韦方程组,可以计算出电感。很多重要案例,经过简化程序后,可以被解析。当涉及高频率电流和伴随的集肤效应,经过解析拉普拉斯方程,可以得到面电流密度与磁场。假设导体是纤细导线,自感仍旧相依于导线半径、内部电流分布。假若导线半径超小于其它长度尺寸,则这电流分布可以近似为常数(在导线的表面或体积内部)。
互感

图上方,闭合回路1的含时电流  所产生的含时磁通量,会促使闭合回路2出现感应电动势
所产生的含时磁通量,会促使闭合回路2出现感应电动势  。图下方,闭合回路2的含时电流
。图下方,闭合回路2的含时电流  所产生的含时磁通量,会促使闭合回路1出现感应电动势
所产生的含时磁通量,会促使闭合回路1出现感应电动势  。
。
如右图所示,流动于闭合回路1的含时电流  ,会产生磁通量
,会产生磁通量  穿过闭合回路2,促使闭合回路2出现感应电动势
穿过闭合回路2,促使闭合回路2出现感应电动势  。穿过闭合回路2的磁通量和流动于闭合回路1的含时电流,有线性关系,称为互感
。穿过闭合回路2的磁通量和流动于闭合回路1的含时电流,有线性关系,称为互感 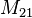 ,以方程表达为。
,以方程表达为。
 。
。
计算互感,可使用纽曼公式(Neumann formula):
 ;
;
其中, 是磁常数,
是磁常数, 是闭合回路1,
是闭合回路1, 是闭合回路2,
是闭合回路2, 是微小线元素
是微小线元素  的位置,
的位置, 是微小线元素
是微小线元素  的位置。
的位置。
由此公式可见,两个线圈之间互感相同: ,且互感是由两个线圈的形状、尺寸和相对位置而确定。
,且互感是由两个线圈的形状、尺寸和相对位置而确定。
导引
穿过闭合回路2的磁通量  为
为
 ;
;
其中, 是边缘为
是边缘为  的任意曲面,
的任意曲面, 是微小面元素。
是微小面元素。
改用磁矢势  计算:
计算:
 ;
;
其中, 是对于变矢量
是对于变矢量  的偏微分。
的偏微分。
应用斯托克斯公式,可以得到
![\Phi_{2}(t)=\int_{\mathbb{S}_2}[\nabla_2\times\mathbf{A}_1(\mathbf{X}_2, t)]\cdot \mathrm{d}\mathbf{a}_2=\oint_{\mathbb{C}_2}\mathbf{A}_1(\mathbf{X}_2, t)\cdot \mathrm{d}\boldsymbol{\ell}_2](http://upload.wikimedia.org/math/8/b/f/8bfea20f7d4496344195cfa75861dc72.png) 。
。
磁矢势  的定义式为
的定义式为
 。
。
磁通量与流动于闭合回路1  的电流
的电流  的关系式为
的关系式为
 。
。
所以,互感为
 。
。
这方程称为纽曼公式(Neumann formula)。注意到对换闭合回路  与
与  不会改变结果,
不会改变结果, ,因此,可以以变量
,因此,可以以变量  统一代表。
统一代表。
类似地,穿过闭合回路1的磁通量  为
为
 。
。
除去所有下标,令  、
、 代表同一闭合回路,自感以方程表示为
代表同一闭合回路,自感以方程表示为
 。
。
当  时,这积分可能会发散,需要特别加以处理。另外,若假设闭合回路为无穷细小,则在闭合回路附近,磁场会变得无穷大,磁通量也会变得无穷大,所以,必须给予闭合回路有限尺寸,设定其截面半径
时,这积分可能会发散,需要特别加以处理。另外,若假设闭合回路为无穷细小,则在闭合回路附近,磁场会变得无穷大,磁通量也会变得无穷大,所以,必须给予闭合回路有限尺寸,设定其截面半径  超小于径长
超小于径长 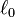 ,
,
有很多种方法可以化解这困难。例如,令  为闭合回路的中心曲轴,令
为闭合回路的中心曲轴,令  为闭合回路的表面,则
为闭合回路的表面,则  ,这积分就不会发散了。
,这积分就不会发散了。
贴片钽电容 AVX贴片钽电容 KEMET贴片钽电容 TO-220封装功率电阻 色环贴片电阻 射频电感 贴片高频电感 光颉电阻 电流采样电阻 高频电感 功率电感 插件电感 磁芯电感
